
Lors d’une visite-atelier à l’Institut du monde arabe, nous avons appris à tracer un pentagone avec la méthode égyptienne : pour cela, nous ne disposions que d’un compas et d’une règle… Nous avons voulu voir si nous parvenions à retrouver les étapes, mais cette fois-ci en utilisant Geogebra, tout en gardant les mêmes contraintes bien sûr.
Au départ, on dispose de deux segments perpendiculaires et de même longueur, [A0H] et [MP], qui se croisent en O.
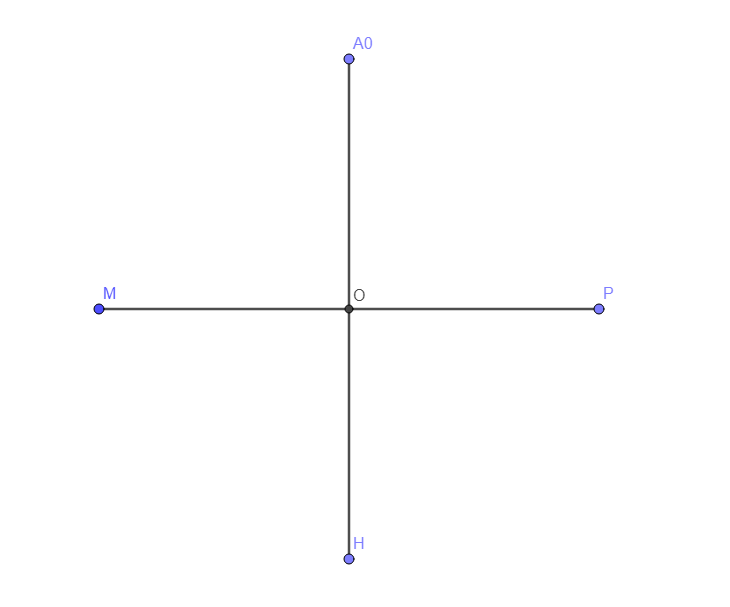
On trace un cercle de centre O et de rayon OP.
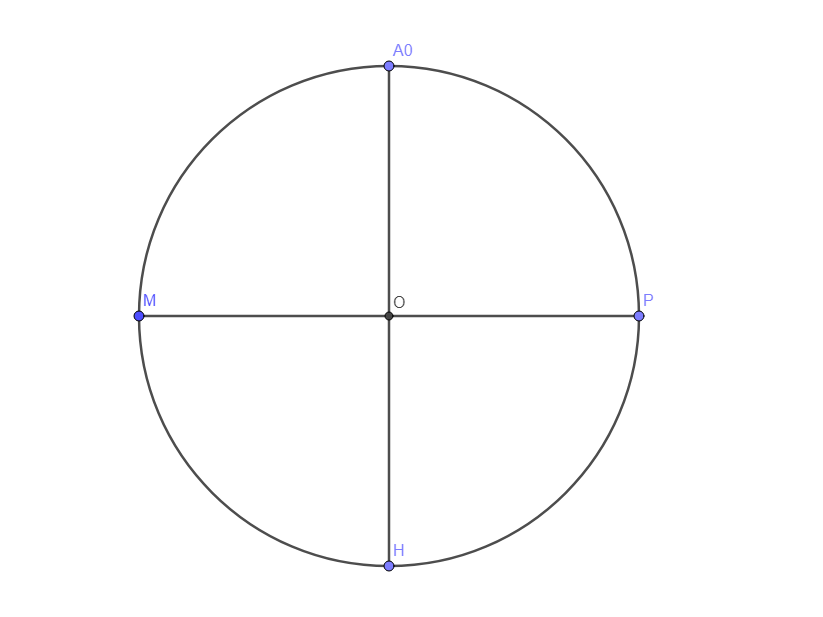
On cherche les milieux R de [MO] et S de [OP].
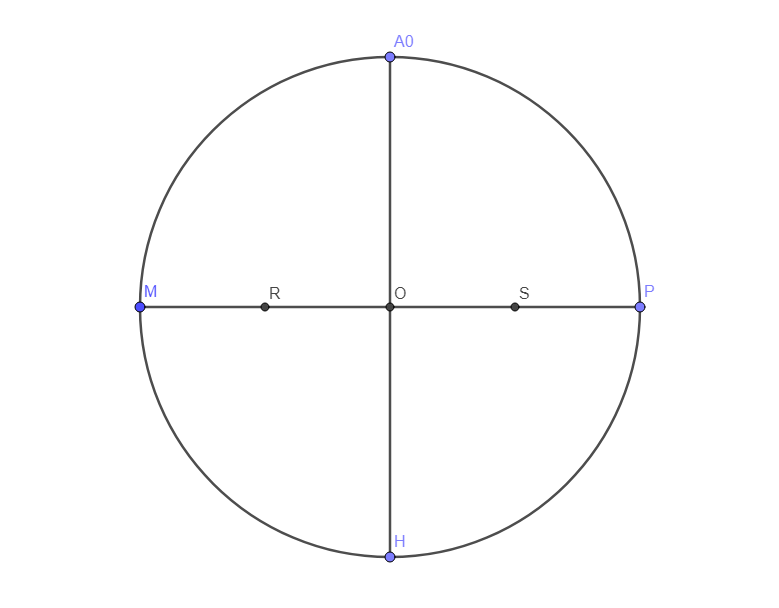
On trace les cercles de centre R et de rayon [RM] et de centre S et de rayon [SP].
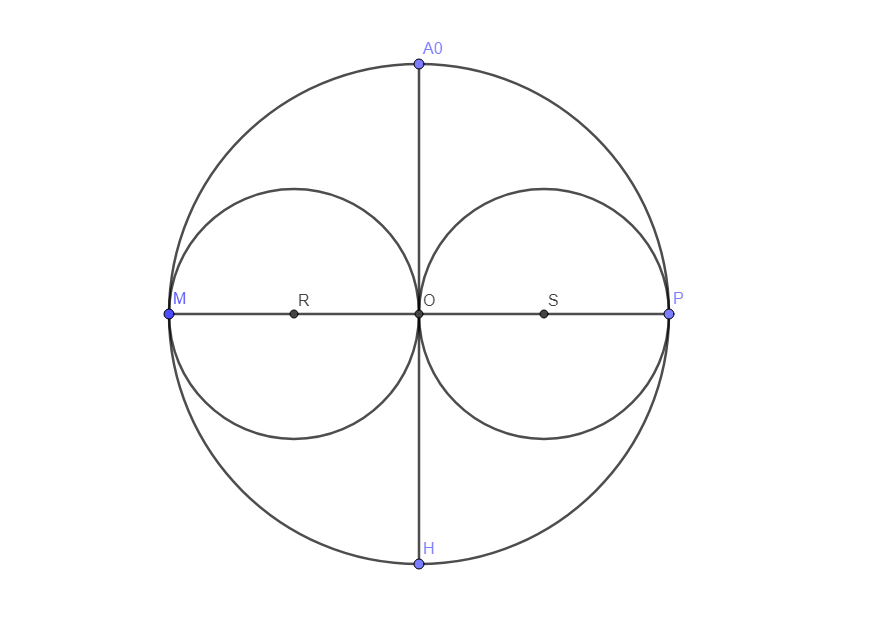
On trace une demi-droite (HS].
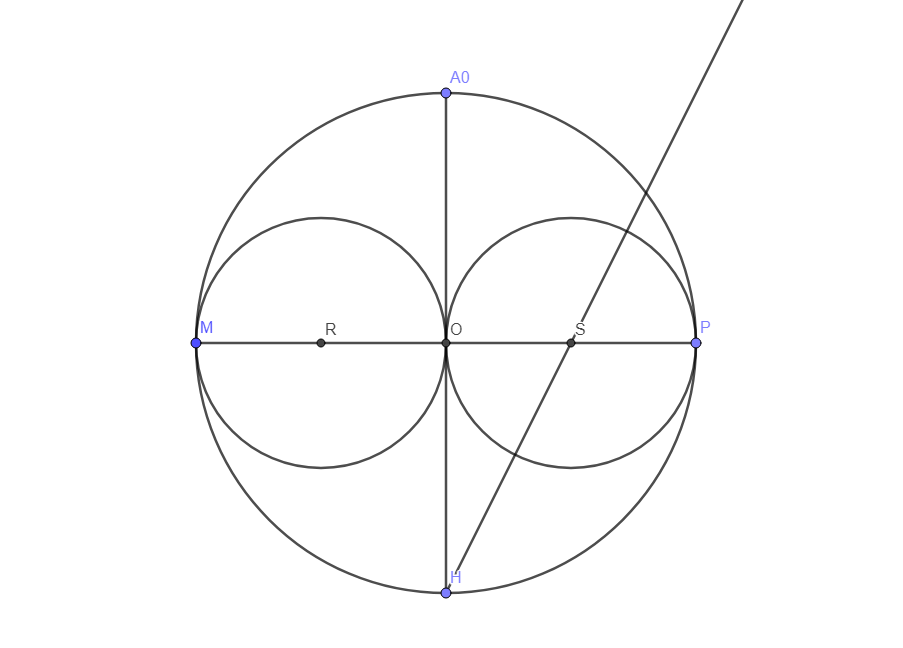
On place T à l’intersection, la plus proche de H, de (HS] et du cercle de centre S.
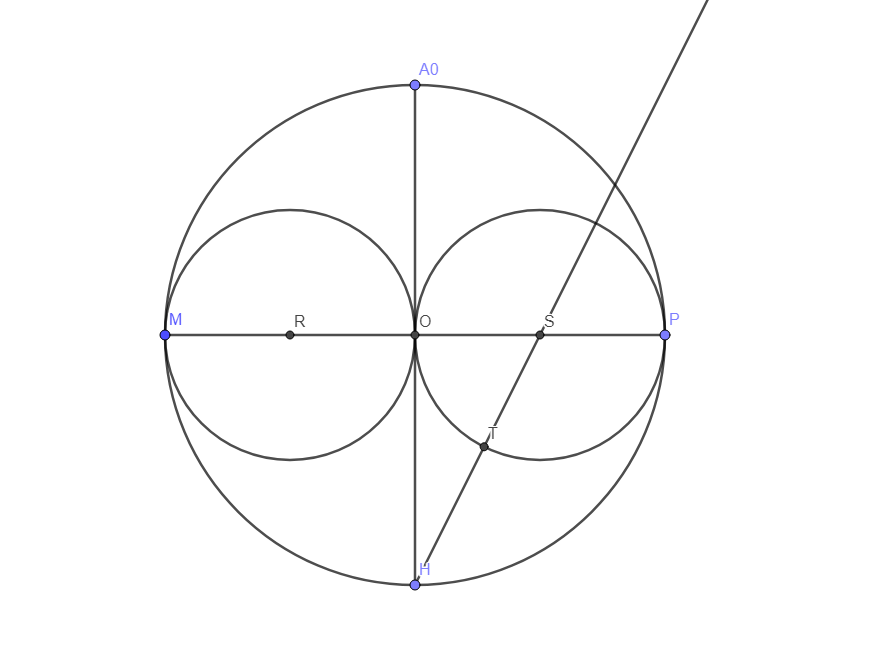
On trace un cercle de centre H et de rayon [HT].
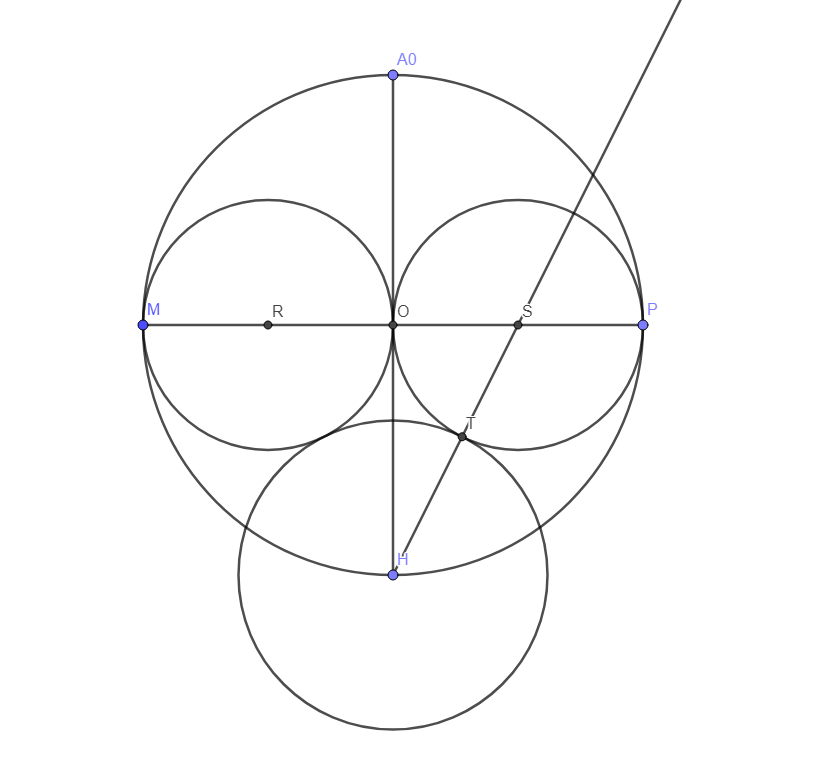
On place U à l’autre intersection de (HS] et du cercle de centre S.
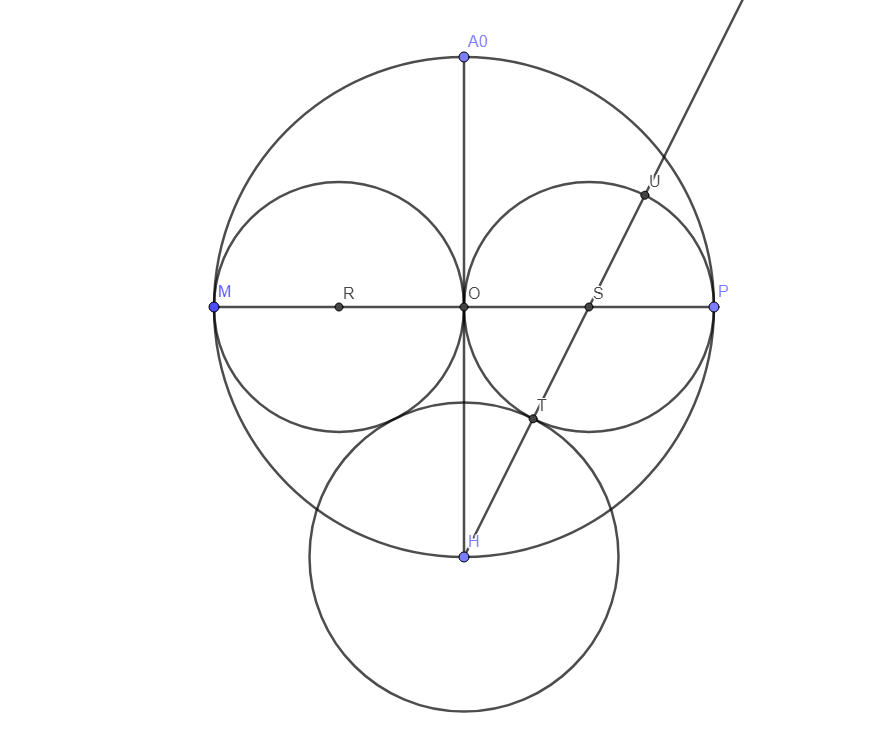
Puis, on trace un cercle (un arc-de-cercle suffit) de centre H et de rayon HU.
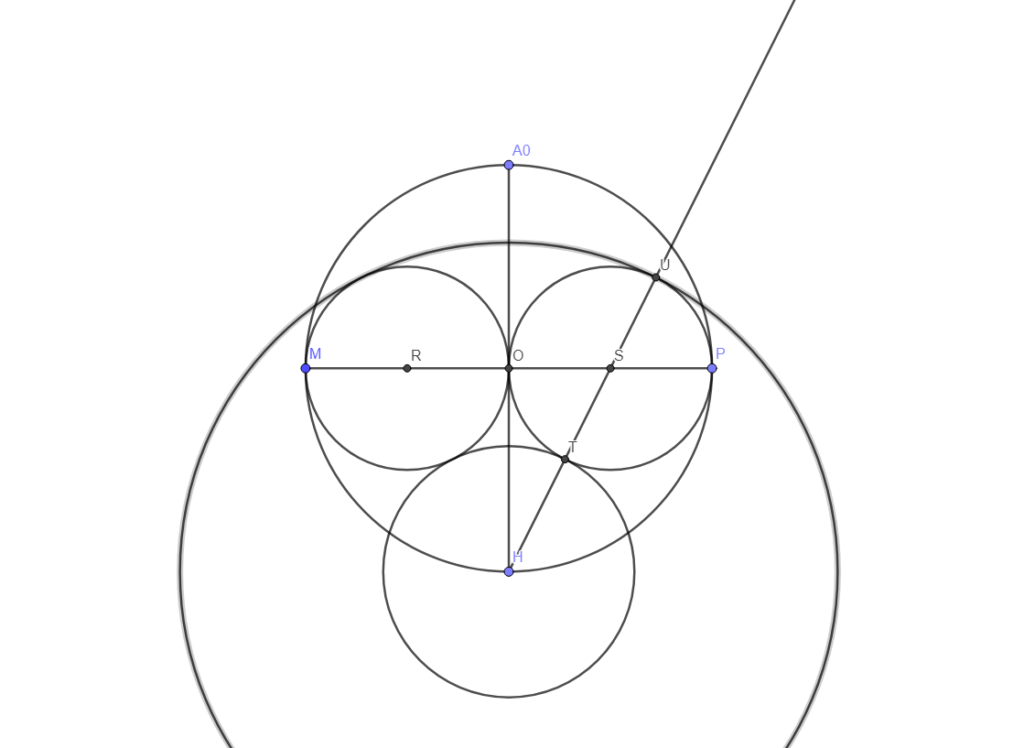
Enfin, on place A1 à l’intersection, sur la droite, de cet arc-de-cercle et du cercle de centre O, A2 à l’intersection sur la droite du cercle de centre O et du cercle de centre H, A3 à l’intersection sur la gauche du cercle de centre H et du cercle de centre O, A4 à l’autre intersection, sur la gauche de l’art-de-cercle et du cercle de centre O.
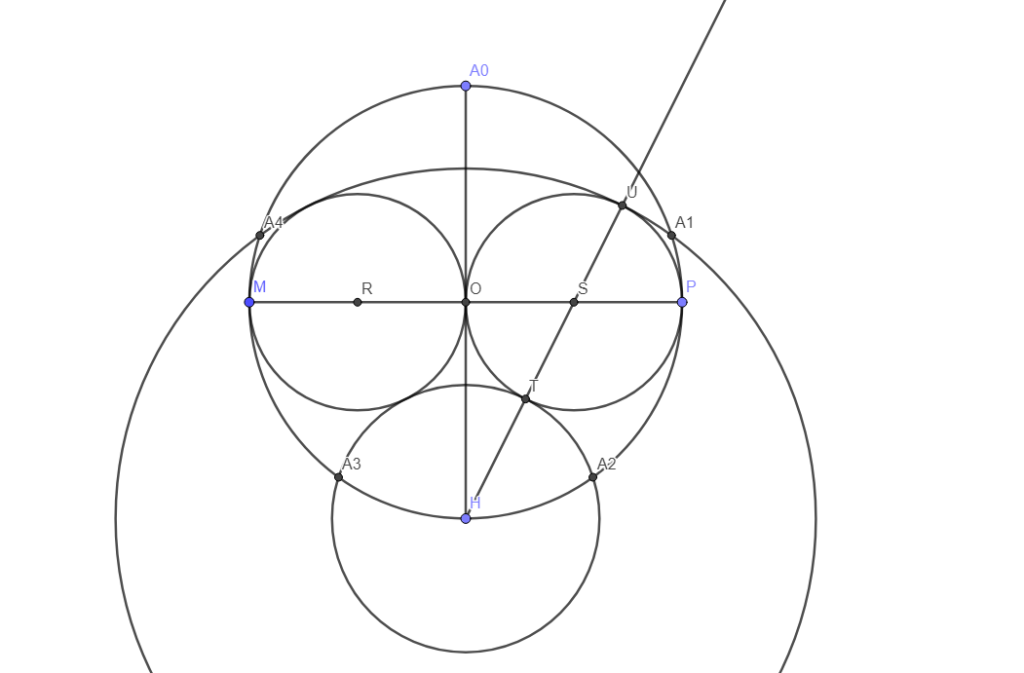
On relie A0, A1, A2, A3 et A4.
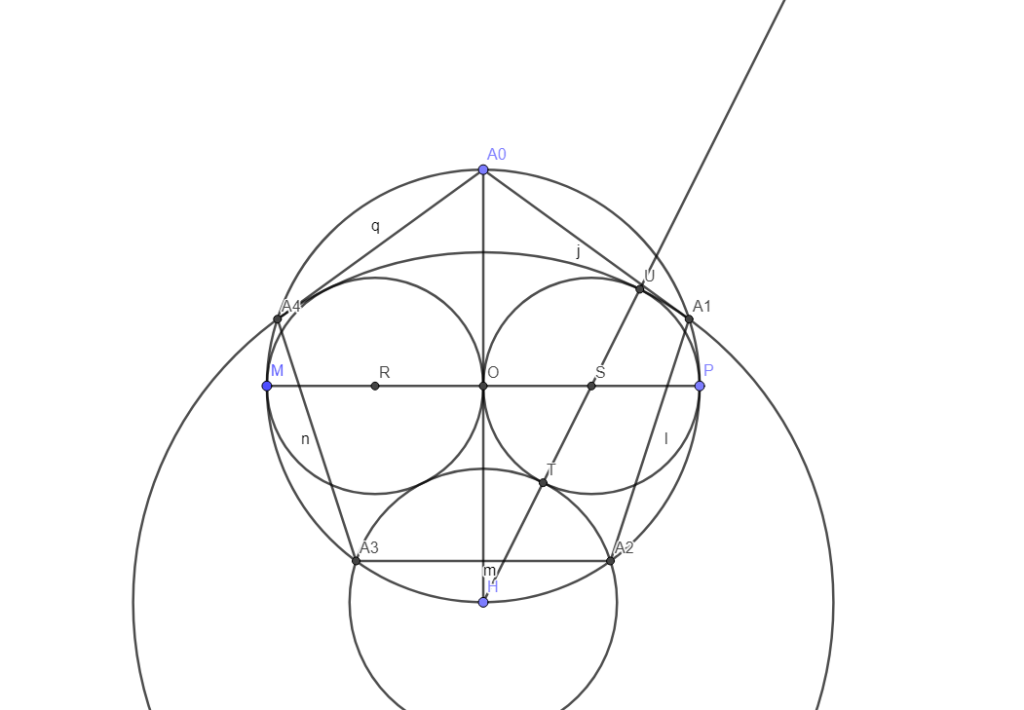
On voit le pentagone apparaître.
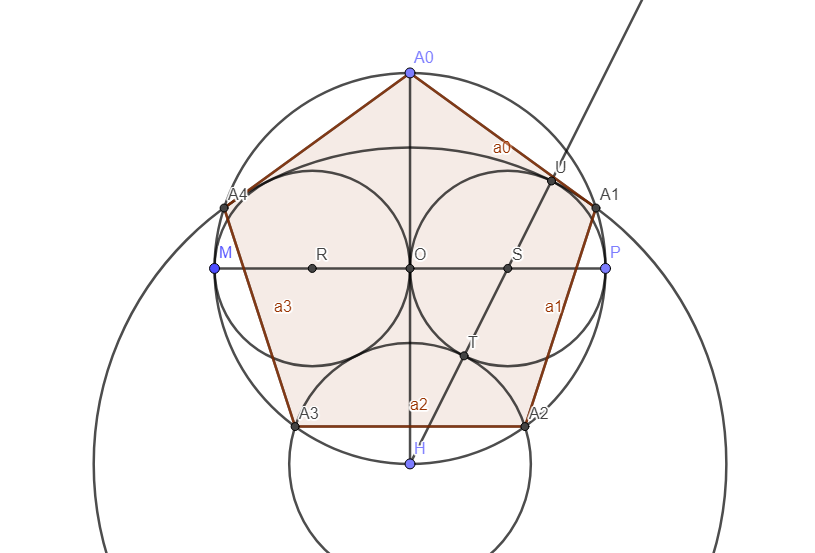
On peut effacer les traits de construction.
C’est fait, avec seulement une règle et un compas !